機械製品はじめハードウェアものの寿命推定には昔からワイブル分布がつかわれてきました。IoT時代に取り沙汰される製品個体ごとの寿命予測と違って、製品設計企画や運用計画で使う期待値的な側面が強い内容ですが、
歴史が長いだけあって手法が様々開発されていたり、
市場データが不完全な場合(truncation)や市場負荷を模擬した耐久試験で打ち切り(censor)がある場合など、
様々なケースを想定していたりするので勉強と思って棚卸しします。
まずは、完全なデータを使う場合を考えます。
データセット
アルミA6061-T6の疲労破壊試験データを使います。データはEngelhardt et al. 1981より孫引きしました[1]。
サンプルデータセット
($ 10^3 $ サイクル単位の破壊寿命(サイクル数); N=101)
70, 90, 96, 97, 99, 100, 103, 104, 104, 105,
107, 108, 108, 108, 109, 109, 112, 112, 113,
114, 114, 114, 116, 119, 120, 120, 120, 121,
121, 123, 124, 124, 124, 124, 124, 128, 128,
129, 129, 130, 130, 130, 131, 131, 131, 131,
131, 132, 132, 132, 133, 134, 134, 134, 134,
134, 136, 136, 137, 138, 138, 138, 139, 139,
141, 141, 142, 142, 142, 142, 142, 142, 144,
144, 145, 146, 148, 148, 149, 151, 151, 152,
155, 156, 157, 157, 157, 157, 158, 159, 162,
163, 163, 164, 166, 166, 168, 170, 174, 196, 212
分布はこの通り
累積ハザード法
Truncationのあるデータにも使える手法で、ワイブル確率紙を使う前提のアナログ信頼性工学では定番だそうです。
手順に従って逆順位から累積ハザード関数H(t)を推定します。手順は[2]を参照。
import pandas as pd
df = pd.DataFrame({'k-cycles':
[70, 90, 96, 97, 99, 100, 103, 104, 104, 105,
107, 108, 108, 108, 109, 109, 112, 112, 113,
114, 114, 114, 116, 119, 120, 120, 120, 121,
121, 123, 124, 124, 124, 124, 124, 128, 128,
129, 129, 130, 130, 130, 131, 131, 131, 131,
131, 132, 132, 132, 133, 134, 134, 134, 134,
134, 136, 136, 137, 138, 138, 138, 139, 139,
141, 141, 142, 142, 142, 142, 142, 142, 144,
144, 145, 146, 148, 148, 149, 151, 151, 152,
155, 156, 157, 157, 157, 157, 158, 159, 162,
163, 163, 164, 166, 166, 168, 170, 174, 196, 212]})
df['reverse-rank']=df.rank(ascending=False)
df['hazard-value']=1/df['reverse-rank']
df['H']=df['hazard-value'].cumsum()
プロットするとこうなります。
ax=df.plot(x='k-cycles', y='H', loglog=True)
ax.grid(True,which='minor')
特性寿命 $ \eta $ と ワイブル係数 $ m $ は、$ H(t) = (t/ \eta)^m $ であるから、$ ln H(t) = m \cdot ln (t) - m \cdot ln(\eta) $ ですね。
import numpy as np
from scipy import stats
df['log-k-cycles']=np.log(df['k-cycles'])
df['log-H']=np.log(df['H'])
slope, intercept, r_value, p_value, std_err = stats.linregress( df['log-k-cycles'], df['log-H'])
print("m:%f, eta:%f"%(slope, np.exp(-intercept/slope)))
プロットはちょっと歪んでますが最小二乗法的に割り当てて、$ ln H(t) = 7.043 ln(t) - 34.934 $ と求まるので、$ \hat{\eta}_{cum} = 143 (10^3 Cycles) $, $ \hat{m}_{cum} = 7.04 $.
メジアン・ランク法
累積ハザード法と異なり全故障での条件でしか使えない方法ですが、累積故障率 $ F(t) $ をメジアン・ランクを用いて推定する手法です。Benard and Bosi-Levenbach (1953) の近似式 $ \frac{i-0.3}{n+0.4} $ を用いて計算します(nは標本サイズ、iは故障順位).
先程と同様にサクサクいきます。手順は[3],[4]を読み解く。
import pandas as pd
import numpy as np
df = pd.DataFrame({'k-cycles':
[70, 90, 96, 97, 99, 100, 103, 104, 104, 105,
107, 108, 108, 108, 109, 109, 112, 112, 113,
114, 114, 114, 116, 119, 120, 120, 120, 121,
121, 123, 124, 124, 124, 124, 124, 128, 128,
129, 129, 130, 130, 130, 131, 131, 131, 131,
131, 132, 132, 132, 133, 134, 134, 134, 134,
134, 136, 136, 137, 138, 138, 138, 139, 139,
141, 141, 142, 142, 142, 142, 142, 142, 144,
144, 145, 146, 148, 148, 149, 151, 151, 152,
155, 156, 157, 157, 157, 157, 158, 159, 162,
163, 163, 164, 166, 166, 168, 170, 174, 196, 212]})
df['rank']=df.rank()
df['F']=(df['rank']-0.3)/(len(df.index)+0.4)
df['1-Finv']=np.log(1/(1-df['F']))
プロットは先ほどと形状があまり変わらないのでスキップ。
特性寿命 $ \eta $ と ワイブル係数 $ m $ に対して、不信頼度 $ F(t) = 1- exp(-\frac{t}{\eta}^m) $ であるから、$ ln ln \frac{1}{1-F(t)} = m \cdot ln (t) - m \cdot ln(\eta) $ ですね。こちらも本来はワイブル確率紙を使う前提の手法ですが手作業簡略化働き方改革で最小二乗法的に特性寿命とワイブル係数求めます。
from scipy import stats
df['log-k-cycles']=np.log(df['k-cycles'])
df['log-log-1-Finv']=np.log(df['1-Finv'])
slope, intercept, r_value, p_value, std_err = stats.linregress( df['log-k-cycles'], df['log-log-1-Finv'])
print("m:%f, eta:%f"%(slope, np.exp(-intercept/slope)))
結果として$ \hat{\eta}_{med} = 143 (10^3 Cycles) $, $ \hat{m}_{med} = 7.18 $.
最尤法(Maximum Likelihood Estimation; MLE)
かつては、解析学を駆使した手法ですが、コンピュータ技術の進展により何の面白みもなくScipyで結果が出るようになってしまいました。シンプルに求めまs。Scipyのドキュメントだけでは、ちょっとわからなかったので[5]を参照。
立式については材料 第24巻 第262号にごっついのが掲載されているので参照してくだされ。
import pandas as pd
import numpy as np
from scipy import stats
df = pd.DataFrame({'k-cycles':
[70, 90, 96, 97, 99, 100, 103, 104, 104, 105,
107, 108, 108, 108, 109, 109, 112, 112, 113,
114, 114, 114, 116, 119, 120, 120, 120, 121,
121, 123, 124, 124, 124, 124, 124, 128, 128,
129, 129, 130, 130, 130, 131, 131, 131, 131,
131, 132, 132, 132, 133, 134, 134, 134, 134,
134, 136, 136, 137, 138, 138, 138, 139, 139,
141, 141, 142, 142, 142, 142, 142, 142, 144,
144, 145, 146, 148, 148, 149, 151, 151, 152,
155, 156, 157, 157, 157, 157, 158, 159, 162,
163, 163, 164, 166, 166, 168, 170, 174, 196, 212]})
# flocはloc(=location)に対してfixed locationの意味。fitで強制的にloc=0にする。
params = stats.exponweib.fit(df, floc=0, f0=1)
m = params[1]
eta = params[3]
print("m:%f, eta:%f"%(m, eta))
結果は$ \hat{\eta}_{mle} = 143 (10^3 Cycles) $, $ \hat{m}_{mle} = 6.07 $.
ベイズ推定
以前mamba.jlを使ったこともありますが、今回はPyMCで行きます。
Reparameterizing the Weibull Accelerated Failure Time Model — PyMC3 3.6 documentationを参考に、$ m $は対数正規分布からサンプリングし、$ \eta $ は、$ m \cdot ln(\eta) $ が正規分布になるようにサンプリング。
import numpy as np
import pymc3 as mc
import pandas as pd
from theano import tensor as T
df = pd.DataFrame({'k-cycles':
[70, 90, 96, 97, 99, 100, 103, 104, 104, 105,
107, 108, 108, 108, 109, 109, 112, 112, 113,
114, 114, 114, 116, 119, 120, 120, 120, 121,
121, 123, 124, 124, 124, 124, 124, 128, 128,
129, 129, 130, 130, 130, 131, 131, 131, 131,
131, 132, 132, 132, 133, 134, 134, 134, 134,
134, 136, 136, 137, 138, 138, 138, 139, 139,
141, 141, 142, 142, 142, 142, 142, 142, 144,
144, 145, 146, 148, 148, 149, 151, 151, 152,
155, 156, 157, 157, 157, 157, 158, 159, 162,
163, 163, 164, 166, 166, 168, 170, 174, 196, 212]})
# Hazard function
def weibull_lccdf(x, m, eta):
return -(x / eta)**m
with mc.Model() as model:
m_sd = 10.0
m_raw = mc.Normal('m0', mu=0, sd=0.1)
m = mc.Deterministic('m', T.exp(m_sd * m_raw))
mu = mc.Normal('mu', mu=0, sd=100)
eta = mc.Deterministic('eta', T.exp(mu/m))
y = mc.Weibull('y', alpha=m, beta=eta, observed=df['k-cycles'])
# 5000イタレーション, バーンイン2000, チェーン数4
with model:
trace = mc.sample(draws=5000, tune=2000,chains=4,
nuts_kwargs={'target_accept': 0.95},
init='adapt_diag')
サンプリング効率が良くないとのエラーが出ますが、先へ進みます。
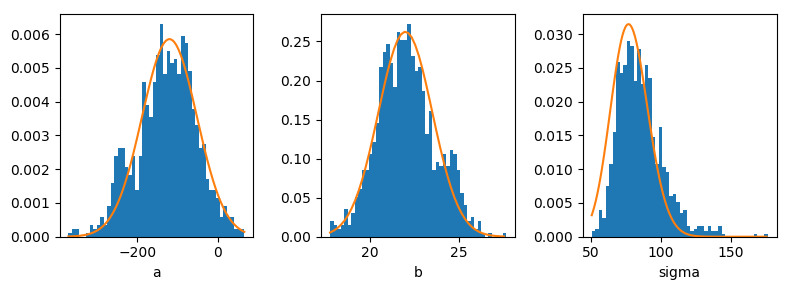
mc.traceplot(trace, varnames=['m', 'eta'])
収束しているようですね。
mc.summary(trace, varnames=['m', 'eta']).round(2)
| |
mean |
sd |
mc_error |
hpd_2.5 |
hpd_97.5 |
n_eff |
Rhat |
| m |
5.98 |
0.41 |
0.01 |
5.16 |
6.76 |
3356.5 |
1.0 |
| eta |
143.14 |
2.54 |
0.02 |
138.23 |
148.23 |
12407.2 |
1.0 |
結果は$ \hat{\eta}_{bay} = 143 (10^3 Cycles) $, $ \hat{m}_{bay} = 5.98 $.
まとめ
点推定値
| |
累積ハザード法 |
メジアン・ランク法 |
最尤法 |
ベイズ推定 |
| $ \eta $ |
143 |
143 |
143 |
143 |
| $ m $ |
7.04 |
7.18 |
6.07 |
5.98 |
サンプル数が100程度と非常に"大きかった"こともあり、特性寿命 $ \eta $は手法によらず143k-Cycle程度。他方でワイブル係数 $ m $ がばらつく。
実運用時には $ B_{10} $ 寿命やMTBF/MTTFを使う必要があるが、これを求める際に、このmのばらつきが大きく影響する。
ISO19973-1/JIS B8672-1 空気圧-試験による機器の信頼性評価の編纂に関わったとする著者のページ信頼性解析(理論編)には、その周辺も含めた知恵への言及があるので、ぜひ読んでみてください。
CDFの比較
Empirical CDFと各手法で推定したパラメータによるCDFをプロット。最尤法とベイズ推定が分布の端っこでEmpirical CDFから乖離している傾向。コードは後述。
信頼性解析ソフトWeibull++のユーザーページによるとMLEで推定したワイブル係数 $ \hat{m}_{mle} $はバイアスしがちだそう[The Weibull Distribution - ReliaWiki].
H. Hirose(1999)の補正式を使うと良くなるらしいので盲目的に試してみたが、サンプル数が十分にある例であるためか補正の結果は目に見えなかった。残念。
プロットのコード
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
df = pd.DataFrame({'k-cycles':
[70, 90, 96, 97, 99, 100, 103, 104, 104, 105,
107, 108, 108, 108, 109, 109, 112, 112, 113,
114, 114, 114, 116, 119, 120, 120, 120, 121,
121, 123, 124, 124, 124, 124, 124, 128, 128,
129, 129, 130, 130, 130, 131, 131, 131, 131,
131, 132, 132, 132, 133, 134, 134, 134, 134,
134, 136, 136, 137, 138, 138, 138, 139, 139,
141, 141, 142, 142, 142, 142, 142, 142, 144,
144, 145, 146, 148, 148, 149, 151, 151, 152,
155, 156, 157, 157, 157, 157, 158, 159, 162,
163, 163, 164, 166, 166, 168, 170, 174, 196, 212]})
def ecdf(data):
n = len(data)
x = np.sort(data)
y = np.arange(1, n+1) / n
return x, y
def weibull_cdf(x, eta, m):
return 1-np.exp(-(x/eta)**m)
x_emp, y_emp = ecdf(df['k-cycles'])
x = np.linspace(np.min(df['k-cycles']), np.max(df['k-cycles']), 50)
y_cum = weibull_cdf(x, 142.54, 7.04)
y_med = weibull_cdf(x, 142.72, 7.18)
y_mle = weibull_cdf(x, 143.16, 6.07)
y_bay = weibull_cdf(x, 143.14, 5.98)
plt.plot(x_emp, y_emp, marker='.', linestyle='none', label='ecdf')
plt.plot(x, y_cum, label='Cum Hazard M curve')
plt.plot(x, y_med, label='Med-Rank curve')
plt.plot(x, y_mle, label='MLE fit curve')
plt.plot(x, y_bay, label='Bayse fit curve')
plt.xlabel('k-cycles')
plt.ylabel('CDF')
plt.legend(['ecdf','Cum-Hazard', 'Med-Rank','MLE','Bayse'])
plt.yticks(np.arange(0, 1.1, step=0.1))
plt.show()
# Hirose
r = 101
y_umle = weibull_cdf(x, 143.16, 6.07/(1.0115+1.278/r+2.001/r**2+20.35/r**3-46.98/r**4))
plt.plot(x_emp, y_emp, marker='.', linestyle='none', label='ecdf')
plt.plot(x, y_mle, label='MLE fit curve')
plt.plot(x, y_umle, label='Unbiased MLE fit curve')
plt.legend(['ecdf','MLE','Unbiased-MLE'])
plt.show()
3パラメータワイブル
廣瀬先生に3パラメータの方が良さそうなデータではないかとコメントを頂いたので試します。
こちらの通り、フィッティングは改善。
パラメータは、特性寿命 $ \hat{\eta}_{mle3} = 80.9 $, 位置パラメータ $ \hat{\theta}_{mle3}=60.9 $, ワイブル係数 $ \hat{m}_{mle3}=3.5 $ です。
結果の解釈をどうしようか迷います。
# 3 params MLE
params = stats.exponweib.fit(df,f0=1,loc=0)
m = params[1]
theta = params[2]
eta = params[3]
2パラメータMLE/ベイズのEmpirical CDFとの乖離はどこから来たか?
別記事で少し掘りました→ワイブル分布パラメータの推定手法の比較 - 夜間飛行
参考
- [1]Inferences on the Parameters of the Birnbaum-Saunders Fatigue Life Distribution Based on Maximum Likelihood Estimation
- サンプルとして使った6061-T6アルミ合金の疲労破壊試験データの引用元。もともとはEstimation for a Family of Life Distributions with Applications to Fatigueのもので、孫引きにあたります。
- [2]ワイブル型累積ハザード解析を用いた除雪機械の故障傾向の把握
- 累積ハザード法の解説
- [3]確率紙による分布推定
- ワイブル確率紙とメジアン・ランク法等の説明。穴埋めになっているところは下記メディアランク表のページなどから穴埋めしてくだされ。
- [4]付表:メディアンランク median rank — 中川雅央(滋賀大学)
- メジアンランク法の補正係数数表
- [5]python – Scipyを使ってワイブル分布を当てはめる - コードログ
- Scipyでワイブル分布の最尤法を行う方法。RやMatlabと結果が違うという不穏な一言が。