問題のおさらい
アヒル本の第4章のデータRStanBook/data-salary.txt を教材に、MCMCのアルゴリズムの勉強を進めています。ことの発端と調査着手の経緯は過去ページをご覧になっていただくとして、ランダムウォーク・メトロポリス・ヘイスティングス法(Random Walk MH法)とハミルトニアン・モンテカルロ法(HMC法)に自分で組みながら単回帰に取り組みましたので その内容をまとめます。
単回帰問題の内容
架空データはB社の社員の年齢X(歳)と年収Y(万円)のデータで、20人分のサンプルがある。このサンプル数20という絶妙なサンプル数の単回帰を行い、予測に使おうという問題です。このうちの予測ではなく、単回帰までのところで、色々やっています。
データ: RStanBook/data-salary.txt
このデータは、$ Y_i \sim \mathcal{N}(a + b \cdot X_i, \sigma^2) $ で表現されるモデルにおいて、最尤法では $ \hat{a} = -119.697 $ , $ \hat{b} = 21.904 $ , $ \hat{\sigma} = 79.099 $ と推定されます。
視覚化のため、プロットもアヒル本の図4.3から拝借してきました(githubへリンク)。このような見た目のデータで、直線は最尤推定によるもの。灰色は信頼性区間。

最尤法に関連したおさらい
傾き $ b $ , 切片 $ a $ に関して、$ n $ をサンプル数とおいたとき、それぞれ、$ \hat{a} \sim \mathcal{N}(a, \sigma^2 \{\frac{1}{n} + \frac{\bar{X}^2}{\sum_{ i = 1 }^{ n } (X_n - \bar{X})^2} \}) $ , $ \hat{b} \sim \mathcal{N}(b, \frac{\sigma^2}{\sum_{ i = 1 }^{ n } (X_n - \bar{X})^2 }) $ , $ \hat{\sigma}^2 \sim \chi_{n-2}^2 \frac{\sigma^2}{n-2} $ ですから、 それぞれの信頼区間は以下の通り。 $$ a \in \left[\hat{a}-t_{\alpha/2,n-2} \hat{\sigma} \sqrt{\frac{1}{n} + \frac{\bar{X}^2}{\sum_{ i = 1 }^{ n } (X_n - \bar{X})^2}}, \hat{a}+ t_{\alpha/2,n-2} \hat{\sigma} \sqrt{\frac{1}{n} + \frac{\bar{X}^2}{\sum_{ i = 1 }^{ n } (X_n - \bar{X})^2}} \right] $$ $$ b \in \left[\hat{b}-t_{\alpha/2,n-2} \frac{\hat{\sigma}}{\sqrt{\sum_{ i = 1 }^{ n } (X_n - \bar{X})^2 }}, \hat{b}+ t_{\alpha/2,n-2} \frac{\hat{\sigma}}{\sqrt{\sum_{ i = 1 }^{ n } (X_n - \bar{X})^2 }} \right] $$ $$ \sigma^2 \in \left[\frac{(n-2)\hat{\sigma}}{\chi^2_{1-\alpha/2}}, \frac{(n-2)\hat{\sigma}}{\chi^2_{\alpha/2}} \right] $$
値を代入して95%信頼区間を計算します。$$ a \in \left[-262.8, 23.5 \right] $$ $$ b \in \left[18.7, 25.1 \right] $$ $$ \sigma^2 \in \left[3572, 13683 \right] $$ $$ \sigma \in \left[59.7, 117.0 \right] $$
参考
証明や理論的背景は、ガウス=マルコフの定理あるいは赤本の第13章を参照お願いいたします。
統計値まとめ(Ground Truth)
以上をMCMC結果のGround Truthとして扱いますので、ここで一旦まとめ (信頼区間と確信区間を同じに扱っていますが、単回帰では数値的に同じになるはず)
| パラメータ名 | 点推定 | 95%信頼区間下限値 | 95%信頼区間上限値 | 標準誤差 |
|---|---|---|---|---|
| a(切片) | -119.7 | -262.8 | 23.5 | 68.15 |
| b(傾き) | 21.9 | 18.7 | 25.1 | 1.52 |
| sigma(残差偏差) | 79.1 | 59.7 | 117.0 |
環境
シミュレーションで使った環境のご紹介。
- Windows 10 - 64bit
- Julia 0.6.1
- mamba 0.11.1
- R 3.4.3
- RTools34
- RStan Version 2.16.2
対数尤度関数(Likelihood function)
対数尤度関数 $ \mathcal{L} (y|a, b, sigma) $ は、こちら。$$ \mathcal{L} (y|a, b, \sigma)=log(\prod_{k=1}^n \mathcal{N}(y_k | a+b \cdot x_k, \sigma^2)) \\= - \frac{n}{2} log(2 \pi) - n \cdot log(\sigma) - \frac{\sum_{k=1}^n (y_k - a - b \cdot x_k)^2}{2 \sigma^2} $$
Distributions.jlを使って書きます。
using Distributions
function likelihood(a, b, sigma)
y_pred = a + b*x
likelihoods = [logpdf(Normal(aa, sigma), bb) for (aa,bb) in zip(y_pred,y)]
l_sum = sum(likelihoods)
return l_sum
end
通常MCMCによるフィッティングでは実施しないかもしれませんが、今回は収束値が最尤法で求められるので、点推定の値を中心に、対数尤度の分布をプロットして分布を確認します。
using Plots
pyplot()
# 点推定の値(を整数に丸めた)
a = -120.0
b = 22.0
sigma = 79.0
# 分布をみる範囲
a_list = collect(-262:24)
b_list = collect(18:0.1:25)
sigma_list = collect(59:117)
ab_list = [likelihood(tmp_a,tmp_b,sigma) for tmp_a in a_list, tmp_b in b_list]
ac_list = [likelihood(tmp_a,b, tmp_sigma) for tmp_a in a_list, tmp_sigma in sigma_list]
cb_list = [likelihood(a, tmp_b,tmp_sigma) for tmp_sigma in sigma_list, tmp_b in b_list]
levels = collect(-160:2.5:-115)
p1 = contour(b_list,a_list,ab_list,levels=levels, xlabel="b", ylabel="a")
p2 = contour(sigma_list,a_list,ac_list, levels=levels, xlabel="sigma", ylabel="a")
p3 = contour(b_list,sigma_list,cb_list, levels=levels, xlabel="b", ylabel="sigma")
plot(p1,p2,p3)
この通り、b(傾き)に対して敏感で、次点でa(切片),最後にsigmaという様子が見られます。後述する通り色々試してみた中ではRandom-Walk Metropolis Hasting法やHMC法では、 この感度が収束に影響を及ぼしているようでした。MCMCにも機械学習に於ける正規化の考え方が必要ということです。

ランダムウォーク=メトロポリス・ヘイスティングス法
アルゴリズムの詳細は触れなくても大丈夫ですよね。おさらい用にリンク貼っておきますね。
- メトロポリス・ヘイスティングス法 - Wikipedia
- Bayesian Inference: Metropolis-Hastings Sampling
- Lecture7: The Metropolis Hastings Algorithm - Nick Whiteley
提案分布
この手法による唯一のチューニング対象(?)はランダムウォークの仕方。酔歩に性格の良い正規分布を使うことを前提にして、分散がチューニングの対象です。 直感的にコーシー・シュワルツの不等式的な発想で各パラメータの事後分布の分散の比率に提案分布が近いとサンプリング効率が良いような気がしています。
function proposal(a, b, sigma)
return [rand(Normal(mu, sd)) for (mu, sd) in zip([a, b, sigma],[80,1,8])]
end試しに提案分布のaの分散をいじります。

どうです。aの標準誤差65に近い80が一番良い雰囲気出していませんか?aの分散を1にしたものと60にしたもので、3000サンプル分のランダムウォークの違いを見てみます。
分散60のほうが心なしか良さそうですよね(点推定値への収束が悪いなぁ)
さらに提案分布を多変量正規分布にすると、より一層良くなりそうな気がしていますが、色々やっておいてなんですが、事前にパラメータの分布がわかっているのも興ざめなので、ここ迄にしておきます。
参考:How to derive variance-covariance matrix of coefficients in linear regression - Cross Validated
メトロポリス・ヘイスティングス法の結果
チューニングしてみましたが(a, b)=(-70, 20.9)など、aが心持ち原点に寄ってくるところが解せないです。初期値を最尤法による点推定の値にしても、aが-70前後に寄ってきてしまうので頭抱えています。 実行のたびに-120を中心に-190~-70でブレるというのならわかるけど、毎回原点側に戻って来てしまうのは、 どういうことなの!?
aが原点に寄る…はっ、桁落ちでは?!
ということで、採択率の計算方法を少し変えました。$$ \alpha = exp(log(p^*) - log(p_t)) $$
を$$ \alpha = \frac{exp(log(p^*))}{exp(log(p_t))} $$ に変えました。
Before
tmp1 = posterior(proposal_draw[1],proposal_draw[2],proposal_draw[3])
tmp2 = posterior(chain[i][1], chain[i][2], chain[i][3])
alpha = min(1,exp(tmp1-tmp2))After
tmp1 = posterior(proposal_draw[1],proposal_draw[2],proposal_draw[3])
tmp2 = posterior(chain[i][1], chain[i][2], chain[i][3])
alpha = min(1,exp(tmp1)/exp(tmp2))
何度か計算させてみても、大体、最尤法の点推定を中心にばらつきます。難点は対数尤度(負の値)が小さすぎるとゼロ割相当になってしまうことでしょうか。

数字で見て見ると $ (a, b, \sigma) = (-122.4, 22.0, 82.2) $ となり、良い!良いです!
mamba.jlでaが小さめに出る問題、桁落ちの可能性もありますね。実際mamba.jlのRandom-Walk MH法では、採択率の計算がこうなっています。きっと同じ症状が出ると思います。
他にもみていくとmamba.jlのHMCにも同じような箇所があり、少し心配になります。NUTSの実装ではHMCを使っていないように見えますので、杞憂かなぁ。
しかし、このような実装がNUTSにも…
不審ですが、これを確認するためHMCに行ってみましょう。
ハミルトニアンモンテカルロ法(HMC)
アルゴリズムについては、ここで、わざわざ書くほどでもないほど、色々な方が記事書いてますし、Stanのマニュアルも充実しています。
短く言うと $ P $ を運動量に見立てて、対数尤度関数をポテンシャル場に使いながら$$ H([a, b, \sigma], [P_a, P_b, P_{\sigma}]) = - likelihood(a, b, \sigma) + \frac{P_{a}^2+P_{b}^2+P_{\sigma}^2}{2} $$ で定義される「ハミルトニアン」を利用して無駄な酔歩を抑えようという感じの発想のアルゴリズムですね。 焼きなまし法みたいに、Iterationのたびにランダムな運動量(≒初速)を与えた玉を少し転がしてやってからサンプリングを繰り返し、 最終的に谷底の中心で跳ね回るようにしていく動作をします。
その効果がこちらのような素早い谷底への到達!!
ポテンシャルエネルギー $ U(a, b, \sigma) = -likelihood(a, b, \sigma) $ 、 運動エネルギー $ K(P_a, P_b, P_{\sigma}) = \frac{P_{a}^2+P_{b}^2+P_{\sigma}^2}{2} $と定義すると、ハミルトニアン $ H = U + K $ になりますね。 これを手を離した振り子の要領で、系のエネルギーを保存しながら、動いてもらおうと思うと、 ハミルトン力学でいうところの正準方程式を数値解法で解いていきます。 これには、シンプレクティックな数値積分法リープ・フロッグ法を使います。
使わないと面倒なことになりそう。
Juliaで単振り子。どうもsolverとしては単純な4次のRunge-Kuttaがいちばん信頼できそうなのだけど、toleranceを調整しても最大振幅の場合はきちんと解けてない。ハミルトン系は1自由度でも難しいな。Symplecticにやればいっぱつなのに pic.twitter.com/3GTXjhtRVT
— きくT(2/10 ビッグアップル) (@kikumaco) December 21, 2017
ということでリープフロッグ法で対数尤度関数の偏微分を使いますので、計算します。$$ \mathcal{L} (y|a, b, \sigma)= - \frac{n}{2} log(2 \pi) - n \cdot log(\sigma) - \frac{\sum_{k=1}^n (y_k - a - b \cdot x_k)^2}{2 \sigma^2} $$ $$ \frac{\partial \mathcal{L} (y|a, b, \sigma)}{\partial a}= \frac{\sum_{k=1}^n (y_k - a - b \cdot x_k)}{\sigma^2} $$ $$ \frac{\partial \mathcal{L} (y|a, b, \sigma)}{\partial b}= \frac{\sum_{k=1}^n x_k (y_k - a - b \cdot x_k)}{\sigma^2} $$ $$ \frac{\partial \mathcal{L} (y|a, b, \sigma)}{\partial \sigma}= -\frac{n}{\sigma} + \frac{\sum_{k=1}^n (y_k - a - b \cdot x_k)^2}{\sigma^3} $$
function dlikelihood(a, b, sigma)
y_pred = a + b*x
grad_a = sum(y - y_pred)/sigma^2
grad_b = dot(x, y - y_pred)/sigma^2
grad_sigma= -1.0/sigma * length(x) + sum(abs2,y - y_pred)/sigma^3
return [grad_a, grad_b, grad_sigma]
endで、Leapfrogの実装は
function Leapfrog(theta, r, epsilon)
r += 0.5 * epsilon * dlikelihood(theta[1], theta[2], theta[3])
theta += epsilon * r
r += 0.5 * epsilon * dlikelihood(theta[1], theta[2], theta[3])
return theta, r
endポテンシャルエネルギーをlikelihoodの-1倍で定義したので、マイナスがキャンセルして"r-="ではなく"r+="になっています。あしからず。
Github →Mamba.jl_Practice/HMC-MassMatrix.ipynb
ステップ数 $ L = 100 $, サンプリング周期 $ \epsilon = 0.2 $ として点推定値付近を50,000 Iterationsほどウロウロさせると、良さそうな雰囲気。
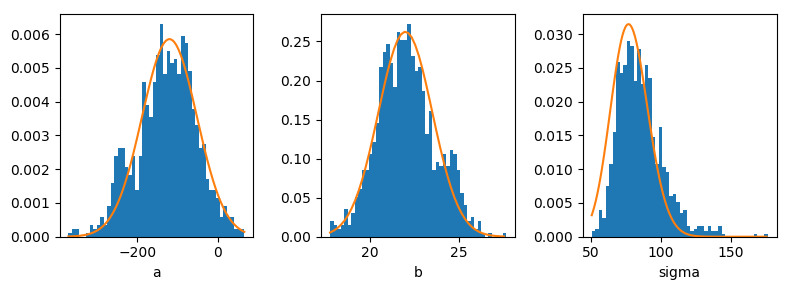
最尤値(オレンジ実線)とサンプリングの比較
$ (mean(a), mean(b), mean(\sigma)) = (-118.0, 21.9, 85.4) $ で、桁落ちの影響もなく良さそうですね。mamba.jlの問題はなんだか、特定できず終いです。
ここまでの話は、この本でカバーされているようなので…ほしいけどゴクリ…。







No comments:
Post a Comment