かなり前にQiitaで2D世界で模擬Lidarを持つロボットの強化学習に取り組みました。元ネタはStanford大学のConvNetJS Deep Q Learning Reinforcement Learning with Neural Network demoで、オリジナルはJavascriptで組まれています。

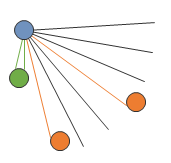
物理エンジンなどは使わず距離計算をしたのですが、そこで使った数学のおさらいをします。

1. 線分の交差

平面世界の外枠やセパレーションを構成する壁までの距離計算です。Lidarの光線長には有効距離があり、壁も有限長なので、それぞれLidarをモデル化した線分と壁をモデル化した線分の交差判定を使います。

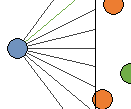
線分が交差する場合の交差点

Lidarの光線1本分と壁を取り出して点O, A, B, Cを下図のように定めます。

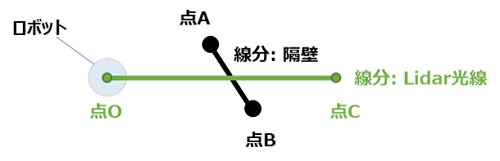
さらに仮に線分が「交差する」とし、交点をPとすれば、点Pが存在することが線分が交差する条件となり、また2点間の距離OPが求めたい「距離」となります。点Pは、$ \vec{OA} $ と $ \vec{OB} $ の内分点であって、$ \vec{OP} $ は $ \vec{OC} $ のスカラー倍です。

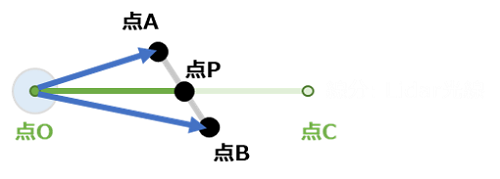
そこで変数 $ s $ と $ t $ を導入して方程式をたてると変数に制約付きの線形方程式になります。

\[ \begin{array}{ll} & s \cdot \vec{OA} + (1-s) \cdot \vec{OB} = t \cdot \vec{OC} \\ {\rm s.t.} & 0 < s < 1 \\ & 0 < t < 1 \\ \end{array} \]

線形方程式のところに注目して $ \vec{OA} = \begin{bmatrix} a_x & a_y \end{bmatrix} ^{\intercal} $, $ \vec{OB} = \begin{bmatrix} b_x, b_y \end{bmatrix} ^{\intercal} $,$ \vec{OC} = \begin{bmatrix} c_x, c_y \end{bmatrix} ^{\intercal} $ と置くと、

\[ \begin{bmatrix} a_x - b_x & - c_x \\ a_y - b_y & - c_y \end{bmatrix} \begin{bmatrix} s \\ t \end{bmatrix} = - \begin{bmatrix} b_x \\ b_y \end{bmatrix} \\ \]

線分が交差する(⇒ 平行でない)ならば、$ \text{det} \begin{bmatrix} a_x - b_x & - c_x \\ a_y - b_y & - c_y \end{bmatrix} \neq 0 $ なので、逆行列をかけて(線形方程式を解いて)、

\[ \begin{bmatrix} s \\ t \end{bmatrix} = \frac{1}{(a_x - b_x) c_y - (a_y - b_y) c_x } \begin{bmatrix} - c_y & c_x \\ - a_y + b_y & a_x - b_x \end{bmatrix} \begin{bmatrix} b_x \\ b_y \end{bmatrix} \\ \]

さらに、$ 0 < s < 1 $ かつ $ 0 < t < 1 $ を満たすとき線分が交差し、点Pは $ \vec{OP} = t \vec{OC} $ で表されます。

交差しない場合とコーナーケース

さて交差する前提で方程式を立てて解を求めましたが、解なしとなる場合や交差状態として特殊な場合について考察します。いずれも線分としては交差しません。

解が求まらないケース

$ \text{det} \begin{bmatrix} a_x - b_x & - c_x \\ a_y - b_y & - c_y \end{bmatrix} = 0 $ のケースでは先の方程式を解けません。このケースでは線分 $ \text{AB} $ と 線分 $\text{OC} $ とが平行ないしは重なっています。

拘束条件の境界あるいは外の場合

$ 0 < s < 1 $ かつ $ 0 < t < 1 $ でない場合、つまり、$ s ≥ 0 $ または $ 1 ≥ s $ または $ t ≥ 0 $ または $ 1 ≥ t $ の場合です。これらの場合は、点Pは、$ \vec{OA} $ と $ \vec{OB} $ の外分点、または$ \vec{OP} $ が $ \vec{OC} $ より長かったり、逆向きだったりします。 境界では、点Pが点O, A, B, Cのいずれかと一致しますが、これは今回は交差なしとして除外してしまいます。

Pythonコード

以上をまとめてPythonコードにします。 $ o = (o[0], o[1]), a = (a[0], a[1]) \dots $ の要領で配列を定義して上記計算をコードに落とします。

def get_intersection(o, a, b, c):
    """
    線分の交点を求める

    Parameters
    ----------
    o : float[2]
        点Oの平面座標
    a : float[2]
        点Aの平面座標
    b : float[2]
        点Bの平面座標
    c : float[2]
        点Cの平面座標

    Returns
    -------
    bool
        線分に交点があるか
    float[2]
        点Pの平面座標。交点がない場合はNone.
  """
    ob = [b[0] -  o[0], b[1] - o[1]]
    oc = [c[0] -  o[0], c[1] - o[1]]
    # oa - ob = ba
    ba = [a[0] -  b[0], a[1] - b[1]]

    det = ba[0] * -oc[1] - ba[1] * -oc[0]

    # 両線分が平行のケース
    if det == 0.0:
        return False, None

    s = - (-oc[1] * ob[0] + oc[0] * ob[1]) / det
    t = - (-ba[1] * ob[0] + ba[0] * ob[1]) / det

    if 0 < s and s < 1.0 and 0 < t and t < 1.0:
        return True, [t*oc[0] + o[0], t*oc[1] + o[1]]

    # 線分に交点がないケース
    return False, None

デモ

上記と同じものをJavascriptに移し替えてCanvasに描いたものがこちらです。隔壁(縦線)が光線を遮っています。

2. 円と線分の交差

報酬のトリガーとなる得点源は円で表現しています。Lidarがこれらまでの距離を測れるように円と線分の交差点を求めます。

円と線分が交差する場合

基本的には線分同士と同じように「交差する」前提で方程式を立てて、解がないケースを検証します。やっかいなケースのほうが共感を集めやすいと思い、光線終点が円の外にあり、交差点が2つあるケースを図にしました。 今回の興味は光線の始点(点O)に近い点Pまでの距離です。 なかなか吸引力のある問題のようでStackoverflowがもりあがっていました。

とはいえ単純に $ \vec{AO} $ と $ \vec{AC} $ の内分点 $ P $ で $ \Vert AP \Vert = r $ となる点を求めるとしてよいですね (ただしrは円の半径)。

\[ \begin{array}{ll} & \Vert s \cdot \vec{AO} + (1-s) \cdot \vec{AC} \Vert = r \\ {\rm s.t.} & 0 < s_0 < 1\\ & s_0 \geq s_1 \\ \end{array} \]

距離の方程式だけに注目して $ \vec{AO} = \begin{bmatrix} o_x & o_y \end{bmatrix} ^{\intercal} $, $ \vec{AC} = \begin{bmatrix} c_x, c_y \end{bmatrix} ^{\intercal} $ と置くと、

\[ \begin{array}{crl} & s^2 (o_x^2 + o_y^2) + 2 s(1-s) (o_x c_x + o_y c_y) + (1-2s+s^2) (c_x^2 + c_y^2) &= r^2 \\ \Leftrightarrow & ((o_x - c_x)^2 + (o_y - c_y)^2) s^2 + 2 (o_x c_x + o_y c_y - c_x^2 - c_y^2) s + (c_x^2 + c_y^2 - r^2) & = 0 \end{array} \]

これは二次方程式なので二次方程式の解の公式 - Wikipediaでも参照してください。

交差しない場合とコーナーケース

解がないケース

「判別式が負になった」が典型的なケースで、これは線分と円が交差しません。また、点Cが円の内部にある場合は $ 0 > s_1 $ となり $ s_0 $ のみが交点です。

拘束条件境界

線分のときと同じ扱いにしました。

Pythonコード

まとめてPythonコードにします。 $ o = (o[0], o[1]), a = (a[0], a[1]) \dots $ の要領で配列を定義して上記計算をコードに落とします。

def get_intersection(o, c, a, r):
    """
    線分の交点を求める

    Parameters
    ----------
    o : float[2]
        点Oの平面座標
    c : float[2]
        点Cの平面座標
    a : float[2]
        円の中心の平面座標
    r : float
        円の半径

    Returns
    -------
    bool
        線分と円に交点があるか
    float[2]
        点Pの平面座標。2つ交点があるときは点Oに近い方。交点がない場合はNone.
  """
    ao = [o[0] - a[0], o[1] - a[1]]
    ac = [c[0] - a[0], c[1] - a[1]]
    co = [o[0] - c[0], o[1] - c[1]]

    eq_a = co[0] ** 2 + co[1]**2
    eq_b = ao[0] * ac[0] + ao[1]*ac[1] - ac[0] ** 2 - ac[1] ** 2
    eq_c = ac[0] **2 + ac[1] ** 2 - r **2

    discriminant = eq_b * eq_b - eq_a * eq_c
    # 解なしのケース
    if discriminant < 0:
        return False, None

    discriminant = discriminant ** 0.5

    s0 = (- eq_b + discriminant)/eq_a
    s1 = (- eq_b - discriminant)/eq_a

    if 0 < s0 and s0 < 1.0:
        return True, [s0 * x + (1 - s0)* y + z for (x, y, z) in zip(ao, ac, a)]

    if 0 < s1 and s1 < 1.0:
        return True, [s1 * x + (1 - s1)* y + z for (x, y, z) in zip(ao, ac, a)]

    # 線分に交点がないケース
    return False, None

デモ

同様にJavascriptに移し替えてCanvasに描いたものがこちらです。ちょっと大きめの円。

参考

• 計算幾何入門
• math - Circle line-segment collision detection algorithm? - Stack Overflow